Les parties 1 et 2 sont dépendantes.

Dans tout ce problème l'espace sera rapporté à un repère orthonormé direct et un point quelconque M de l'espace sera repéré par ses coordonnées cartésiennes (x, y, z).

On considère une lame chargée en volume limitée par les plans d'équations respectives x = -h et x = +h (où e est une constante positive désignant l’épaisseur de la lame) et infinie dans les directions de Oy et de Oz (figure 1).

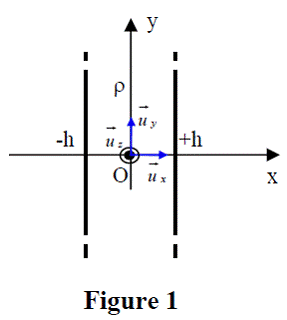
La lame est chargée uniformément en volume avec une densité ρ positive. Soit  et V1(M) le champ et le potentiel électrostatiques créés en M par cette distribution de charges.

1) De quelles variables d'espace, le potentiel V1(M) dépend t-il ?

2) Déduire la forme des surfaces équipotentielles et des lignes de champ.

3) Montrer que

4) Calculer le champ à l'aide du théorème de Gauss en tout point M de l'espace.

5) Déduire le potentiel V1(M). On prendra V1(0, 0, 0) = 0.

6) Tracer les courbes de variations de E1 et V1 en fonction de z.

7) On se place dans le cas où l'épaisseur 2h est "très faible". La distribution de charges est alors assimilée au plan (Oxy) chargé surfaciquement avec une densité uniforme σ.

    a) Exprimer la densité surfacique σ en fonction de ρ et h.

    b) Déduire l'expression du champ et du potentiel électrostatiques créés par le plan chargé.

    c) Tracer les courbes de variations de en fonction de z.

8) Une distribution de charges sur un plan infini ou dans une tranche infinie peut-elle exister dans la réalité?

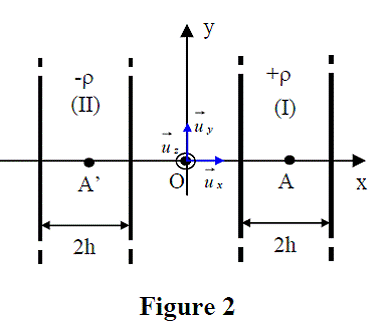
On considère maintenant la distribution de charges représentée sur la figure 2 comprenant deux lames (I et II) infinies dans les directions y et z, d’épaisseur 2h, centrées en A et A’, d'abscisses respectives +a et -a ( a > h ), et de charges volumiques uniformes ρ et - ρ. On désigne par le champ électrostatique crée par la lame de centre A et celui crée par la lame de centre A’.

1) a) Montrer que le plan x = 0 est un plan de symétrie impair pour les deux lames.

     b) En déduire que le champ crée par les deux lames est une fonction paire de x :

2) a) Donner les expressions de EI (M) et EII (M) dans les trois cas suivants :

cas a) : x ≥ a + h , cas b) : a − h ≤ x ≤ a + h et cas c) 0 ≤ x ≤ a − h .

    b) Déterminer les expressions du champ résultant dans les trois cas a), b) et c).

    c) Tracer alors l’allure de  en fonction de x.

3) a) Montrer que où  est le potentiel associé aux deux lames.

    b) Donner les expressions de dans les trois cas a), b) et c).

    c) tracer l’allure de  en fonction de x.

➨Voir La solution