0. Introduction :un peu d’histoire

Le mot vient du grec « trigone » (triangle) et « metron » (mesure).

Dans l‘Encyclopédie (1751), Jean le Rond d‘Alembert (1717 ; 1783) définit la trigonométrie comme :

« l‘art de trouver les parties inconnues d‘un triangle par le moyen de celles qu‘on connaît ».

C‘est bien la démarche qui est demandée aux élèves du collège.

I. Relations trigonométriques dans le triangle rectangle :

Theoreme : Dans un triangle rectangle ABC, on peut définir les relations suivantes entre les angles aigus et les différentes longueurs des côtés.

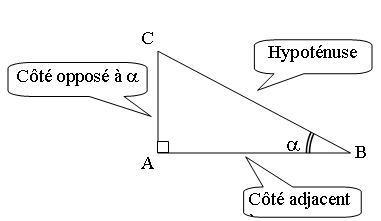
Définition :

– Le cosinus d’un angle aigu est donné par:

– Le sinus d’un angle aigu est donné par :

– La tangente d’un angle aigu est donnée par :

Moyen mnémotechnique :

  SOH-CAH-TOA

Expliquations:

CAH: Cos()= (longueur du cote Adjacent a l’angle ) : (longueur de l’Hypotenuse )

SOH: Sin()= (longueur du cote Opposé a l’angle ) : (longueur de l’Hypotenuse )

TOA: Tan()= (longueur du cote Opposé a l’angle ): (longueur du cote Adjacent a l’angle )

Remarques :

– Le sinus et le cosinus d‘un angle sont toujours compris entre – 1 et 1.

– Par contre, la tangente d‘un angle aigu peut prendre toutes les valeurs.

Exemples :

Si AC=16 cm et BC=20 cm, calculer .

[ Réponse :  =0,8]

Si AC=16 cm et AB= 12 cm, calculer

[ Réponse :   =1,33]

II. Détermination de la mesure d’un angle en degré, connaissant son cox ou sinx ou tanx :

Méthode:

La détermination de la mesure d‘un angle connaissant son cosx, sinx ou tanx s‘effectue à l‘aide de la calculatrice en utilisant les touches :

En ayant verifie, prealablement, que la calculatrice est en mode degre

Exemples :

• Si cos x = 0,5 alors

• Si sin x = 0,5 alors

• Si tan x = 1 alors

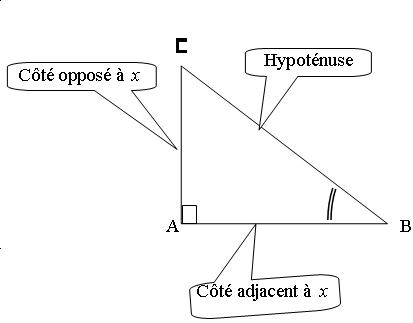
III. Formules Trigonométriques :

Propriétés :

Pour tout angle x, les égalités suivantes sont toujours vraies :

Preuve :

Or ABC est rectangle en A, donc d‘après la partie directe du théorème de Pythagore : AB²+AC²=BC²

D‘où :

Puis