2.5 Les fonctions affines
Dans cette leçon, nous considérerons comme acquis le chapître sur les fonctions linéaires .
On se placera dans un repère .
I.Les fonctions affines :
1.Activité d‘introduction :
Considérons un rectangle de longueur x cm et de largeur 3 cm.

Notons y son périmètre.
Nous allons étudier les variations du périmètre en fonction de celles de la longueur.
a. Compléter le tableau de valeur suivant :
| Longueur (en cm) | 1 | 2 | 4 | 5 |
| Périmètre (en cm) | 8 | 10 | 14 | 16 |
b. Ce tableau représente-t-il une situation de proportionnalité ?
c. Le périmètre est-il une fonction linéaire de la longueur du rectangle ?
d. Donner une relation (égalité) reliant y et x.
On dit que le périmètre (y) est une « fonction affine » de la longueur (x).
Nous avons y =2x+ 6 d‘après la formule du périmètre d‘un rectangle
e. Dans le repère (O, , placer les points A(1,8) B(2 ;10) C(4 ;14) D(5 ;16).

f. Quelles sont vos remarques ?
Tous les points sont alignés sur une droite.
2. Définition :
Définition :
Soient a et b deux nombres relatifs donnés.
La fonction affine f de coefficients a et b est définie par la relation :
A tout nombre x on associe le nombre ax+b.
On note ( où f définie par f(x)=ax+b)
Le nombre f(x) est appelé image de x par la fonction f.
Exemples :
Dans l‘activité précédente la périmètre est une fonction affine f de la longueur.
En notant x la longueur. O
n a f(x)= 2x+6 avec a=2 et b=6.
Si a = 3 et b = -5 alors la fonction affine est : .
Calculer l‘image des nombres 2 et -3 par f.
donc l‘image de 2 par f est 1.
Remarque :
Une fonction linéaire est une fonction affine puisqu‘elle s‘écrit avec b=0.
La réciproque est fausse.
Une fonction affine n‘est pas toujours linéaire.
Contre-exemple : est affine mais pas linéaire.
3. Courbe représentative d‘une fonction affine :
Dans l‘activité d‘introduction, nous avons remarqué que la courbe est une droite,
Cette propriété est généralisée pour toutes les fonctions affines. Propriété :
La représentation graphique d‘une fonction affine est une droite.
Cette droite a pour équation réduite y=ax+b.
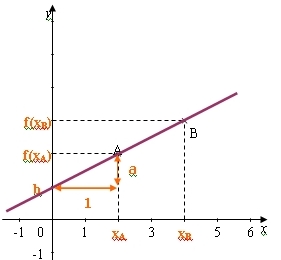
a est appelé « le coefficient directeur »
et b « l‘ordonnée à l‘origine ».
Remarque :
b s‘appelle l‘ordonnée à l‘origine car f(0)=ax0+b=b donc la droite passe par le point de coordonnées (0,b) donc par l‘ordonnée à l‘origine.
Exemple :
Représenter graphiquement .
Méthode :
Le principe est le même que pour les fonctions linéaires.
Sauf que dans ce cas il nous faut deux points.
Prenons deux valeurs de x différentes et calculons leur image.
| Valeur de x | 0 | 2 |
Valeur de f(x) | 2 | 8 |
| Points de la droite | A(0;2) | B(2;8) |
II.Détermination de l‘expression d‘une fonction affine par le calcul :
Méthode :
Le procédé est similaire à celui des fonctions affines sauf que dans ce cas nous avons deux coefficients (a et b) déterminer donc il nous faut deux informations donc les coordonnées de deux points.
Exemple :
Déterminer l‘expression de la fonction f dont la courbe passe par les points A(2,5) et B (-1 ;-1)
y= ax+b
A appartient à la droite donc ses coordonnées vérifient l‘équation 5=2a+b.
B appartient à la droite donc ses coordonnées vérifient l‘équation -1=-1a+b.
Nous sommes donc amenés à résoudre le système suivant :
Après résolution, nous obtenons a =2 et b=1.
Conclusion :
La fonction f recherchée est : .
Remarque :
b s‘appelle l‘ordonnée à l‘origine car donc la droite passe par le point de coordonnées (0,b) donc par l‘ordonnée à l‘origine.
Si le chapitre sur les systèmes n‘a pas été étudié,
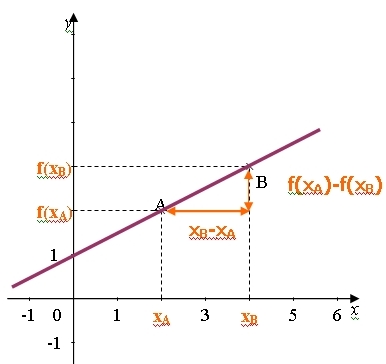
a est le coefficient de proportionnalité entre les accroissements de
f(x) et ceux de x donc pour tout nombres et
distincts
Donc
et b s‘obtient en résolvant ou
.
Retrouvons l‘expression de la fonction f par cette méthode :
ensuite
5=2a+b
5=2×2+b
b=5-4=1
ou
-1=2x(-1)+b
-1=-2+b
b=-1+2=1
Conclusion :
nous retrouvons bien a=2 et b=1 donc .

