Examen N°3

L’espace physique est rapporté à un repère orthonormé direct 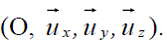Un point M de l’espace est repéré dans la base cylindrique par (r, θ, z).

A/ On considère un cylindre creux (S) de rayon R, de longueur infinie, chargé en surface par une densité surfacique de charges uniforme σ > 0 (figure 1). Soit M un point quelconque de l’espace.

1) Indiquer les coordonnées dont dépend le champ électrostatique et déterminer sa direction.

2) a) Définir et justifier la surface de Gauss.

    b) Déterminer le champ en tout point M de l’espace (r < R et r > R).

3) a) Tracez l’allure de E(r) en fonction de r (où E(r) est la norme du champ).

    b) Le champ est-il continu à la traversée de la surface du cylindre.

4) En prenant comme référence du potentiel V(r = 0) = V0, calculez le potentiel V(r) en tout point M de l’espace.

5) a) Tracez l’allure de V(r) en fonction de r.

    b) Vérifier que le potentiel V(r) est continu à la traversée du cylindre.

B/ Une couronne cylindrique (C) d’axe  et de rayon intérieur R1 et extérieur R de longueur infinie, porte une charge volumique répartie entre les surfaces des deux cylindres avec une densité constante ρ > 0 (figure 2).

6) Précisez les invariances du champ électrostatique et déterminer sa direction.

7) a) En utilisant le théorème de Gauss, donner les expressions du champ électrostatique en tout point M de l’espace.

    b) Le champ est-il continu à la traversée des deux surfaces de la couronne cylindrique (C).

8) On fait tendre R1 → R, la charge totale de la distribution volumique de la couronne cylindrique est alors répartie sur la surface d’un cylindre creux de longueur infinie et de rayon R. Soit σ la densité de charges du cylindre creux.

    a) Exprimer σ en fonction de ρ, R1 et R.

    b) Retrouver les expressions de crée par un cylindre creux.

9) On se place maintenant dans le cas où R1 = 0 et on suppose que le rayon R est négligeable devant la longueur du cylindre chargé. La charge totale de la distribution volumique peut être considérée répartie uniformément sur un fil infini. On désigne par λ la densité linéique du fil.

    a) Exprimer λ en fonction de ρ et R.

    b) En déduire l’expression du champ crée par le fil.

    c) Retrouver crée par un fil de longueur infinie à partir du théorème de Gauss.

    d) En déduire l’expression du potentiel V(M) crée par le fil infini à une constante additive près qu’on notera K.

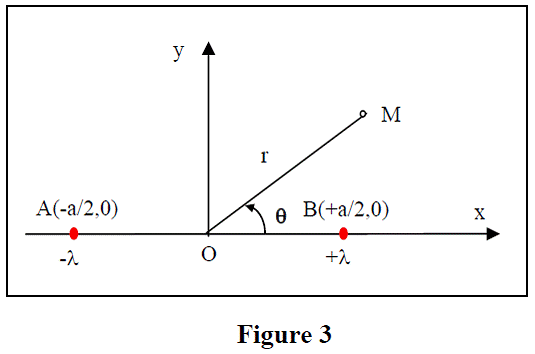C/ On considère deux C/ On considère deux fils rectilignes, de longueurs infinies, portant des distributions linéiques de charges de densités constantes +λ et −λ (λ > 0). Ces deux fils sont parallèles entre eux et perpendiculaire au plan (Oxy). On désigne par A(-a/2, 0) et B(+a/2, 0) les intersections respectives du fil chargé ( −λ ) et celui chargé à ( +λ ) avec le plan (Oxy).

L’origine O du repère (Oxy) est le milieu de AB (AB = a), (figure 3). Soit M un point du plan (Oxy) repéré en coordonnées polaires par (r, θ) avec r = OM et .

On désigne par V(M) et respectivement le potentiel et le champ électrostatique crées par les deux fils en un point M très éloigné des fils : r >> a .

10) En utilisant les résultats de B-9-d), donner les expressions du potentiel crée par le fil en A et du potentiel  crée par le fil en B (à constante additive près).

11) Sachant que le point O est pris comme origine du potentiel : V(O) = 0 , en déduire l’expression du potentiel V(M) crée par les deux fils.

12) Dans le cadre de l’approximation dipolaire (r >> a), exprimer les distances AM et BM en fonction de r, a et θ.

13) a) Montrer que :

       b) Montrer que les deux fils chargés se comportent comme un dipôle électrostatique isolé dont on précisera le moment dipolaire p .

14) En déduire les composantes radiale et orthoradiale du champ électrostatique , son module et sa direction.

 ➨Voir La solution